تحلیل جریان مش (آنالیز جریان مش با حل مثال)

تجزیه و تحلیل شبکه مدار و کشف جریان یا ولتاژ کار دشواری است. با این حال، اگر فرآیند مناسبی را برای کاهش پیچیدگی اعمال کنیم، تجزیه و تحلیل مدار آسان خواهد بود. تکنیک های اساسی تحلیل شبکه مدار پایه، تحلیل جریان مش و تحلیل ولتاژ گره ای است.
تحلیل مش و گره
تحلیل مش و گره ای دارای یک سری قوانین خاص و معیارهای محدود برای گرفتن نتیجه ای عالی از آن هستند. برای کار مدار، ولتاژ منفرد یا چندگانه یا منبع جریان یا هر دو مورد نیاز است. تعیین تکنیک آنالیز، گام مهمی در حل مدار است و این به تعداد ولتاژ یا منبع جریان موجود در مدار یا شبکه های خاص بستگی دارد.
تحلیل مش به منبع ولتاژ موجود بستگی دارد، در حالی که تحلیل گره به منبع جریان بستگی دارد. بنابراین، برای محاسبه ساده تر و کاهش پیچیدگی، استفاده از تحلیل مش در جایی که تعداد زیادی منبع ولتاژ در دسترس است، انتخاب عاقلانه تری است. در عین حال اگر مدار یا شبکه ها با تعداد زیادی از منابع جریان سرو کار داشته باشند، بهترین انتخاب تحلیل گره است.
اما اگر یک مدار هم منبع ولتاژ داشته باشد و هم جریان، چه می شود؟ اگر یک مدار دارای تعداد زیادی ولتاژ و تعداد کمی منبع جریان باشد، تحلیل مش بهترین انتخاب است، اما نکته اصلی این است که منابع جریان را به یک منبع ولتاژ معادل تبدیل کنید.
پیشنهاد میشود برای یادگیری تحلیل گره در مدار، مقاله آموزش تحلیل ولتاژ گره را بخوانید.
در این آموزش، ما در مورد تحلیل مش بحث خواهیم کرد و نحوه استفاده از آن را در شبکه مدار خواهیم فهمید.
روش تحلیل جریان مش
برای تحلیل شبکه با تجزیه و تحلیل مشروط، شرایط خاصی باید تحقق یابد. تحلیل مش فقط برای مدار ها یا شبکه های برنامه ریز کاربرد دارد.
مدار مسطح چیست؟
مدار برنامه ریز یک مدار یا شبکه ای ساده است که می تواند در سطح یک هواپیما کشیده شود و هیچ کراس اووری اتفاق نمی افتد. هنگامی که مدار به یک کراس اوور نیاز دارد، آنگاه آن یک مدار غیرهمسطح است.
در زیر تصویر یک مدار مسطح نشان داده شده است. این یک مداری ساده است و هیچ کراس اووری در آن وجود ندارد.
اکنون مدار زیر، یک مداری غیرهمسطح است. با وجود کراس اوور در مدار نمی توان مدار را ساده کرد.
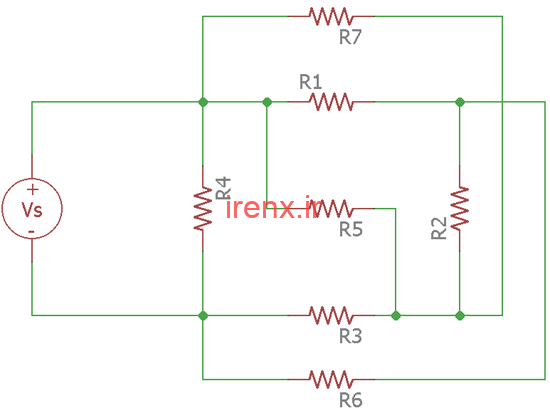
تحلیل مش را نمی توان در مدار غیر مسطح انجام داد و فقط می تواند در مدار مسطح انجام شود. برای استفاده از تحلیل مش، چند مرحله ساده برای رسیدن به نتیجه نهایی لازم است.
- اولین قدم این است که تشخیص دهید مدار مسطح است یا غیر همسطح
- اگر این یک مدار مسطح است، باید بدون هیچگونه کراس اووری ساده شود.
- شناسایی مش ها
- شناسایی منبع ولتاژ
- یافتن مسیر گردش جریان
- اعمال قانون کیرشهوف در مکانهای مناسب
بیایید ببینیم که چگونه تحلیل مش می تواند یک فرایندی موثر برای تجزیه و تحلیل سطح مدار باشد.
یافتن جریان در مدار با روش جریان مش
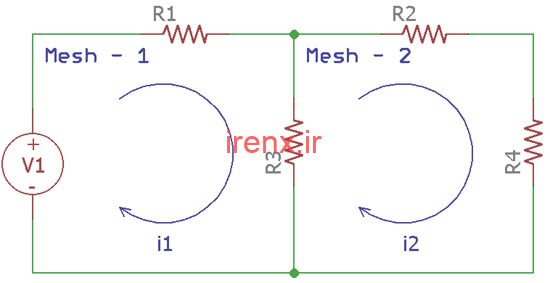
مدار فوق شامل دو مش است. این یک مدار برنامه ریز ساده است که در آن 4 مقاومت وجود دارد. مش اول با استفاده از مقاومت های R1 و R3 و مش دوم با استفاده از R2، R4 و R3 ایجاد می شود.
دو مقدار متفاوتی از جریان از هر شبکه عبور می کند. منبع ولتاژ V1 است. جریان در حال گردش در هر مش را می توان با استفاده از معادله مش به راحتی تشخیص داد.
برای مش اول، V1، R1 و R3 به صورت سری به هم متصل می شوند. بنابراین، هر دو جریان یکسانی دارند که به عنوان شناسه گردش آبی به نام i1 نشان داده می شود. برای مش دوم، دقیقاً همان اتفاق می افتد، R2، R4 و R3 همان جریان را دارند که همچنین به عنوان یک خط گردش آبی نشان داده می شود، که به عنوان i2 نشان داده می شود.
یک مورد استثنا برای R3 وجود دارد. R3 یک مقاومت مشترک بین دو مش است. این بدان معنی است که دو جریان مختلف از دو مش متفاوت از طریق مقاومت R3 جریان دارند. جریان R3 چقدر خواهد بود؟ این تفاوت بین دو شبکه یا جریان حلقه است. بنابراین، جریان از طریق مقاومت R3 i1 – i2 است.
بیایید مش اول را در نظر بگیریم.
با استفاده از قانون ولتاژ کیرشهوف، ولتاژ V1 برابر با اختلاف ولتاژ R1 و R3 است.
حالا ولتاژ R1 و R3 چقدر است؟ برای این مورد، قانون اهم بسیار مفید خواهد بود. مطابق قانون اهم، ولتاژ = مقاومت x جریان.
بنابراین، برای R1 ولتاژ i1 x R1 و برای مقاومت R3 است، (i1 – i2) x R3 خواهد بود
بنابراین، طبق قانون ولتاژ کیرشهوف ،
V1 = i1R1 + R3(i1 – i2)………..[Equation: 1]
برای مش دوم، هیچ منبع ولتاژی مانند V1 در مش اول وجود ندارد. در چنین حالتی، طبق قانون ولتاژ کیرشهوف، در مسیر شبکه مدار حلقه بسته، اختلافات پتانسیل همه مقاومت ها برابر با 0 است.
بنابراین، با استفاده از همان قانون اهم و کیرشهوف ،
با حل معادله 1 و معادله 2 می توان مقدار i1 و i2 را فهمید. اکنون دو مثال عملی برای حل حلقه های مدار خواهیم دید.
R3(i1 – i2)) + i2R2 + i2R4 = 0)………..[Equation: 2]
حل مثال تحلیل جریان مش
جریان مش در مدار زیر چقدر خواهد بود؟
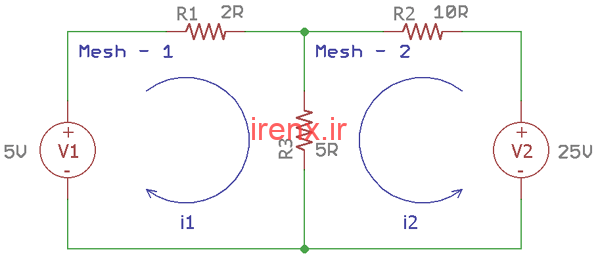
شبکه مدار بالا نسبت به مثال قبلی کمی متفاوت است. در مثال قبلی، مدار دارای منبع ولتاژ منفرد V1 است، اما برای این شبکه مدار، دو منبع ولتاژ متفاوت وجود دارد، V1 و V2. در مدار دو مش وجود دارد.
برای مش 1، V1، R1 و R3 به صورت سری وصل می شوند. بنابراین، جریان مشابهی از طریق سه جزء i1 جریان دارد.
با استفاده از قانون اهم، ولتاژ هر جزء برابر است با
V1 = 5V VR1 = i1 x 2 = 2i1
برای R3، دو جریان حلقه از آن عبور می کند زیرا این یک جزء مشترکی بین دو مش است. از آنجا که دو منبع ولتاژ متفاوت برای مش های مختلف وجود دارد، جریان در مقاومت R3 برابر i1 i2 است.
بنابراین، ولتاژ در
VR3 = (i1+i2) x 5 = 5(i1+i2)
طبق قانون کیرشهوف ،
V1 = 2i1 + 5(i1+i2) 5 = 7i1 + 5i2……. (Equation:1)
اکنون در مش 2، V2، R2 و R3 به صورت سری وصل شده اند. بنابراین، جریان مشابهی از طریق سه جزء جریان می یابد که i2 است.
با استفاده از قانون اهم، ولتاژ هر جزء می باشد :
V1 = 25V VR2 = i2 x 10 = 10i2 VR3 = (i1 + i2) x 5 =5(i1 + i2)
طبق قانون کیرشهوف :
V2 = 10i2 + 5(i1+i2) 25 = 5i1+15i2 5 = i1+ 3i2….. (Equation: 2)
بنابراین، در اینجا دو معادله 5 = 7i1+ 5i2 و 5 = i1+ 3i2 وجود دارد.
با حل این دو معادله ما داریم :
i1 = .625A i2 = 1.875A
مدار بیشتر در ابزار PSpice شبیه سازی شد تا نتیجه را ارزیابی کند.
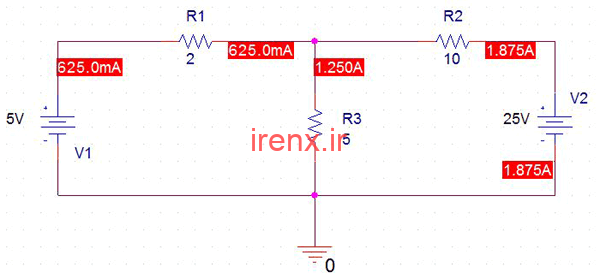
دقیقاً همان مدار در Orcad Pspice تکرار می شود و ما همان نتیجه را می گیریم.
حل سه مش با تحلیل جریان مش
در اینجا یکی دیگر از نمونه های کلاسیک تحلیل مش است
بیایید شبکه مدار زیر را در نظر بگیریم. با استفاده از تحلیل مش، سه جریان را در سه مش محاسبه خواهیم کرد.
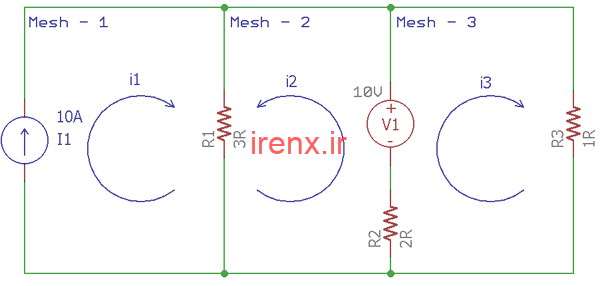
شبکه مدار فوق دارای سه مش است. یک منبع جریان اضافی نیز وجود دارد.
برای حل شبکه مدار در فرآیند تحلیل مش، مش 1 به عنوان i1 نادیده گرفته می شود، یک منبع جریان ده آمپری خارج از شبکه مدار است.
در مش 2، V1، R1 و R2 به صورت سری به هم متصل می شوند. بنابراین، جریان مشابهی از طریق سه جزء جریان می یابد که آن i2 است.
با استفاده از قانون اهم، ولتاژ هر جزء می باشد :
V1 = 10V
برای R1 و R2، از هر مقاومت دو جریان حلقه جریان دارد. R1 یک جز مشترک بین دو مش 1 و 2 است. بنابراین جریانی که از طریق مقاومت R1 جریان می یابد i2 – i2 است. همانند R1، جریان سراسر مقاومت R2 برابر i2 – i3 است.
بنابراین، ولتاژ روی مقاومت R1 :
VR1 = (i2 – i1) x 3 = 3 (i2 – i1)
و برای مقاومت R2 :
VR2 = 2 x (i2 – i3) = 2(i2 – i3)
طبق قانون کیرشهوف ،
3(i2 – i1) + 2(i2 – i3) + 10 = 0 or -3i1 + 5i2 = -10…. (Equation: 1)
بنابراین، مقدار i1 از قبل مشخص شده است که 10A است.
با دادن مقدار i1 می توان معادله 2 را تشکیل داد.
-3i1 + 5i2 – 2i3 = -10 -30 + 5i2 – 2i3 = -10 5i2 – 2i3 = 20…. (Equation: 2)
در مش 3، V1، R3 و R2 به صورت سری به هم متصل می شوند. بنابراین، جریان مشابهی از طریق سه جزء جریان می یابد که i3 است.
با استفاده از قانون اهم، ولتاژ هر جزء برابر است با :
V1 = 10V VR2 = 2 (i3 – i2) VR3 = 1 x i3 = i3
طبق قانون کیرشهوف :
i3 + 2 (i3 – i2) = 10 or, -2i2 + 3i3 = 10….[Equation:3]
بنابراین، در اینجا دو معادله 5i2 – 2i3 = 20 و 2i2 3i3 = 10 وجود دارد. با حل این دو معادله، i2 = 7.27A و i3 = 8.18A.
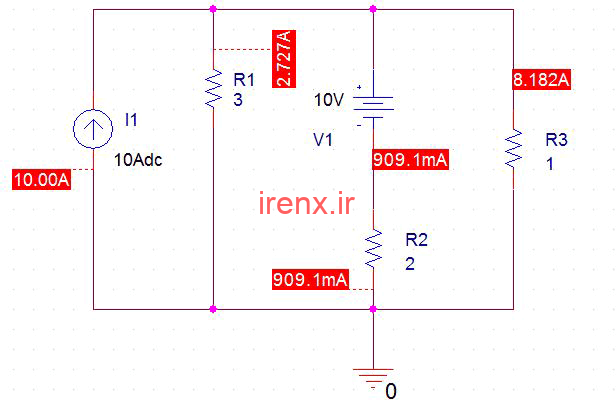
شبیه سازی آنالیز مش در pspice همان نتیجه محاسبه شده مشابه را نشان داد.
بدین ترتیب می توان جریان را در حلقه ها و مش ها را با استفاده از تحلیل جریان مش محاسبه کرد.