سلف های سری و موازی (محاسبه اندوکتانس معادل)

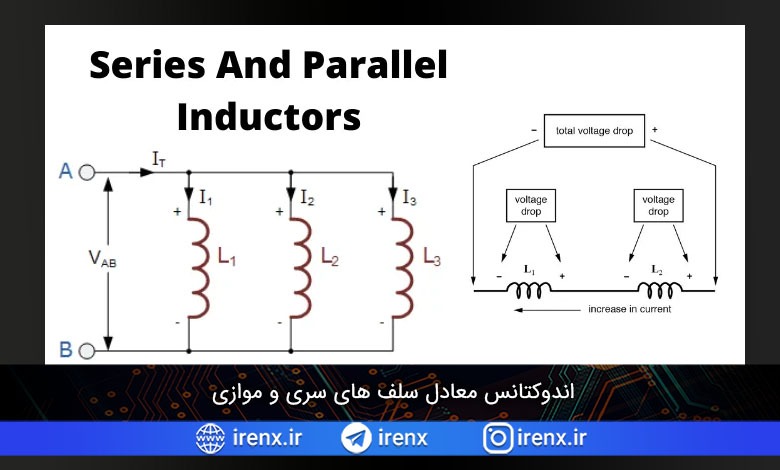
هنگامی که سلف ها به صورت سری به هم متصل می شوند، اندوکتانس معادل، مجموع اندوکتانس همه سلف ها خواهد بود. اندوکتانس معادل برای سلف های سری دقیقاً مانند بدست آوردن مقاومت معادل برای اتصال سری است.

اما در مورد سلف ها گاهی اوقات باید اثر اندوکتانس متقابل بین سلف ها را نیز در نظر بگیریم.

سپس برای محاسبه اندوکتانس هر سلف، هم اندوکتانس خودی و هم اندوکتانس متقابل سلف را جمع کنیم.

بسته به قطبیت سلف ها، اندوکتانس متقابل به اندوکتانس خودی اضافه یا از آن کم می شود.

در ادامه این مقاله با تأثیر اندوکتانس متقابل آشنا خواهیم شد.

حال، بدون در نظر گرفتن اندوکتانس متقابل، می توانیم اندوکتانس معادل سلف هایی که به صورت سری بهم متصل شده اند را به صورت زیر بنویسیم:

هنگامی که سلف ها به صورت موازی به هم متصل می شوند، معکوس اندوکتانس معادل، مجموع اندوکتانس های معکوس هر سلف خواهد بود. اندوکتانس معادل برای سلف های موازی دقیقاً مانند بدست آوردن مقاومت معادل برای اتصال موازی است. همچنین در صورت لزوم ممکن است مجبور باشیم اثر اندوکتانس متقابل را نیز برای مشخص کردن اندوکتانس کل در نظر بگیریم.

در ادامه این مقاله با تأثیر اندوکتانس متقابل بر سلف های موازی آشنا خواهیم شد. بدون در نظر گرفتن اثر اندوکتانس متقابل،  می توانیم بنویسیم:

بیایید اندوکتانس معادل سلف های سری و موازی را بدست آوریم:

سلف های سری

شکل زیر با n تعداد سلف های سری متصل شده را در نظر بگیرید.

• اندوکتانس سلف 1 و افت ولتاژ در آن به ترتیب L1 و v1 است.
• اندوکتانس سلف 2 و افت ولتاژ در آن به ترتیب L2 و V2 است.
• اندوکتانس سلف 3 و افت ولتاژ در آن به ترتیب L3 و v3 است.
• اندوکتانس سلف 4 و افت ولتاژ در آن به ترتیب L4 و v4 است.
• اندوکتانس سلف n و افت ولتاژ در آن به ترتیب Ln و vn هستند.

اکنون، با اعمال قانون ولتاژ کیرشهف، افت ولتاژ کل (v) را در سراسر ترکیب سری سلف ها بدست می آوریم:

افت ولتاژ در یک سلف با اندوکتانس L را می توان به صورت زیر بیان کرد:

که i جریان لحظه ای عبوری از سلف است.

از آنجایی که تمام سلف‌ ها به صورت سری به هم متصل هستند، جریان عبوری از همه سلف‌ ها یکسان و برابر i است. بنابراین، از معادله KVL بالا، به دست می آوریم:

این معادله را می توان به صورت زیر بازنویسی کرد:

که Leq اندوکتانس معادل سلف های سری است. بنابراین داریم:

اندوکتانس معادل سلف هایی که به صورت سری متصل شده اند، برابر با مجموع حسابی اندوکتانس تمام‌ سلف ها است.

سلف های موازی

شکل زیر با n تعداد سلف های موازی متصل شده را در نظر بگیرید.

• اندوکتانس سلف 1 و جریان عبوری از آن به ترتیب L1 و i1 است.
• اندوکتانس سلف 2 و جریان عبوری از آن به ترتیب L2 و i2 است.
• اندوکتانس سلف 3 و جریان عبوری از آن به ترتیب L3 و i3 است.
• اندوکتانس سلف 4 و جریان عبوری از آن به ترتیب L4 و i4 است.
• اندوکتانس سلف n و جریان عبوری از آن به ترتیب Ln و in است.

اکنون، با اعمال قانون جریان کیرشهف، جریان کل (i) برای ترکیب موازی سلف ها برابر است با:

جریان عبوری از یک سلف L را می توان به صورت زیر بیان کرد:

که v ولتاژ لحظه ای در دو طرف سلف است.

از آنجایی که همه سلف ها به صورت موازی به هم متصل شده اند، افت ولتاژ تمام سلف ها یکسان و برابر v است. بنابراین، از معادله KCL بالا، داریم:

این معادله را می توان به صورت زیر بازنویسی کرد:

که Leq اندوکتانس معادل سلف ها با ترکیب موازی است. بنابراین داریم:

معکوس اندوکتانس معادل سلف های موازی برابر مجموع حسابی معکوس اندوکتانس تمام سلف ها است.

اثر اندوکتانس متقابل در سلف های سری

زمانی‌ که بیشتر از یک سلف داشته باشیم، ممکن است بین آنها اندوکتانس متقابل وجود داشته باشد. اگر بیش از یک سلف به صورت سری به هم متصل شده باشند و شار یک سلف، سلف دیگر را به آن پیوند دهد، باید در محاسبات اندوکتانس معادل، اندوکتانس متقابل را نیز در نظر بگیریم.

برای بدست آوردن اندوکتانس متقابل از قرارداد نقطه ای استفاده می کنیم. در اینجا هر یک از سلف ها با یک نقطه در یک انتهای آن مشخص شده است.

جریانی که از سر نقطه ‌دار یک سلف وارد می ‌شود، باعث القای ولتاژ در سلف دیگر با قطبیت مثبت در طرف نقطه ‌دار سلف می‌ شود. مثال زیر را در نظر بگیرید.

از آنجایی که سلف ها به صورت سری متصل هستند، جریان یکسانی از همه سلف ها عبور می کند.

بنابراین وقتی جریان به سر نقطه‌ دار سلف 1 وارد می‌ شود، به سر نقطه‌ دار سلف 2 نیز وارد می ‌شود.

سلف 2 ولتاژ دو طرف سلف 1 را با قطبیت مثبت در انتهای نقطه دار سلف 1 القا می کند.

جریان ورودی از سر نقطه‌ دار سلف 1 باعث القای ولتاژ در سلف 2 با قطبیت مثبت در انتهای نقطه‌ دار سلف 2 می ‌شود.

از آنجایی که EMF های القایی متقابل در جهت امپدانس های معادل EMF خودالقایی هستند، برای محاسبه امپدانس معادل، اندوکتانس متقابل به اندوکتانس خودی اضافه می شود.

در مثال دوم، طبق قرارداد نقطه‌ ای که در شکل زیر نشان داده شده است، جریان الکتریکی از سر نقطه ‌دار یک سلف وارد می ‌شود و همان جریان از سر نقطه‌ دار سلف دیگر خارج می‌ شود.

در آن صورت قطبیت emf القایی متقابل با emf خود القایی متفاوت است. بنابراین اندوکتانس معادل برابر خواهد بود با:

اندوکتانس متقابل در سلف های موازی

در اینجا به اثر اندوکتانس متقابل در سلف های موازی می پردازیم. در این مثال، نقطه هایی به یک سمت دو سلف داده می شود.

هنگامی که جریان از سر نقطه‌ دار سلف 1 وارد می‌ شود، emf القا شده دارای قطبیت مثبت در انتهای نقطه‌ دار سلف 2 است.

به طور مشابه، وقتی جریان از سر نقطه ‌دار سلف 2 وارد می ‌شود، emf القا شده در سلف 1 دارای قطبیت مثبت در انتهای نقطه ‌دار سلف 1 است. بنابراین اندوکتانس معادل برابر است با:

به همین ترتیب، هنگامی که دو سلف موازی به روش زیر نقطه گذاری شوند، اندوکتانس معادل برابر خواهد بود با: